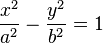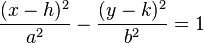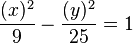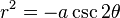Hipérbola
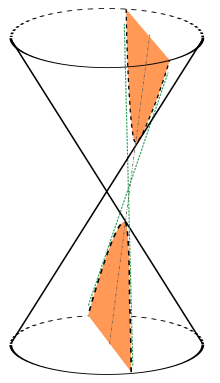
Una hipérbola (del griego ὑπερβολή) es una sección cónica, una curva abierta de dos ramas obtenida al cortar un cono recto por un plano oblicuo al eje de simetría con ángulo menor que el de la generatrizrespecto del eje de revolución.1
|
 [editar]Etimología. Hipérbole e hipérbola
[editar]Etimología. Hipérbole e hipérbola
Hipérbola deriva de la palabra griega ὑπερβολή (exceso), y es cognado de hipérbole (la figura literaria que equivale a exageración).
Véase también: hipérbole
[editar]Historia
Según la tradición, las secciones cónicas fueron descubiertas por Menecmo, en su estudio del problema de la duplicación del cubo,2 donde demuestra la existencia de una solución mediante el corte de una parábola con una hipérbola, lo cual es confirmado posteriormente por Proclo y Eratóstenes.3
Sin embargo, el primero en usar el término hipérbolafue Apolonio de Perge en su tratado Cónicas,4considerada obra cumbre sobre el tema de las matemáticas griegas, y donde se desarrolla el estudio de las tangentes a secciones cónicas.
[editar]Ecuaciones de la hipérbola
Ecuaciones en coordenadas cartesianas: Ecuación de una hipérbola con centro en el origen de coordenadas 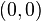 y ecuación de la hipérbola en su forma compleja.
y ecuación de la hipérbola en su forma compleja.
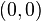 y ecuación de la hipérbola en su forma compleja.
y ecuación de la hipérbola en su forma compleja.Ecuación de una hipérbola con centro en el punto 

Ejemplos:
a)
b)
Ecuación de la hipérbola en su forma compleja
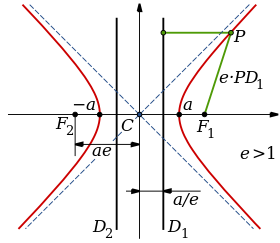
Una hipérbola en el plano complejo es el lugar geométrico formado por un conjunto de puntos  , en el plano
, en el plano  ; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias
; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias 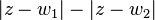 , a dos puntos fijos llamados focos
, a dos puntos fijos llamados focos y
y  , es una costante positiva igual al doble de la distancia (osea
, es una costante positiva igual al doble de la distancia (osea  ) que existe entre su centro y cualesquiera de sus vértices del eje focal.
) que existe entre su centro y cualesquiera de sus vértices del eje focal.
 , en el plano
, en el plano  ; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias
; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias 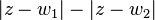 , a dos puntos fijos llamados focos
, a dos puntos fijos llamados focos y
y  , es una costante positiva igual al doble de la distancia (osea
, es una costante positiva igual al doble de la distancia (osea  ) que existe entre su centro y cualesquiera de sus vértices del eje focal.
) que existe entre su centro y cualesquiera de sus vértices del eje focal.La ecuacion queda: 

Evidentemente esta operación se lleva a cabo en el conjunto de los números complejos.
[editar]Ecuaciones en coordenadas polares
Hipérbola abierta de arriba a abajo:
Hipérbola abierta de noroeste a sureste:
[editar]Ecuaciones paramétricas
Hipérbola abierta de derecha a izquierda:
Hipérbola abierta de arriba a abajo: